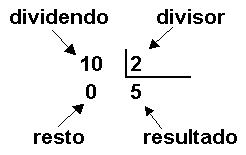
Elementos da Divisão

Elementos da Divisão

A divisão é uma das operações matemáticas fundamentais, sendo a inversa da multiplicação. Ela consiste em dividir um número (dividendo) em partes iguais, com base em um divisor. O resultado da divisão é chamado de quociente, e, dependendo da divisão, pode ocorrer um resto. Vamos entender melhor os elementos da divisão e como ela funciona.

1. O que é a divisão?

A divisão é o processo de distribuir uma quantidade total em partes iguais. Se você tiver uma quantidade de itens e quiser dividir esses itens igualmente entre algumas pessoas, a operação que você usa é a divisão.

Por exemplo, se você tem 12 balas e quer distribuí-las igualmente entre 4 pessoas, você faz a divisão de 12 por 4. A operação seria:

12 ÷ 4 = 3

Isso significa que cada pessoa receberá 3 balas.

2. Elementos da Divisão

Na operação de divisão, temos 4 componentes principais:

• Dividendo (D): O número que será dividido.
• Divisor (d): O número pelo qual o dividendo será dividido.
• Quociente (Q): O resultado da divisão.
• Resto (r): O que sobra após a divisão, se a divisão não for exata.

A fórmula geral da divisão pode ser expressa como:

$$D÷d=Q\text{com resto}r$$

Exemplo:

Considerando a divisão 17 ÷ 5:

• Dividendo (D): 17
• Divisor (d): 5
• Quociente (Q): 3 (pois 17 ÷ 5 = 3)
• Resto (r): 2 (pois sobra 2 após dividir 17 por 5)

A operação seria representada como:

$$17÷5=3\text{com resto}2$$

Ou, de maneira formal:

$$17=(5\times 3)+2$$

3. Divisão Exata x Divisão Inexata

Quando a divisão não deixa resto, ou seja, o dividendo é exatamente divisível pelo divisor, dizemos que a divisão é exata.

Exemplo de divisão exata:

$$20÷4=5$$

Aqui, 20 ÷ 4 não deixa resto, e o quociente é 5.

Por outro lado, se a divisão deixa um número que não pode ser dividido igual entre as partes, temos uma divisão inexata, como no exemplo anterior (17 ÷ 5), onde o quociente é 3, mas sobra um resto de 2.

4. A Divisão com Restos

Nem toda divisão é exata. Quando não há uma divisão exata entre o dividendo e o divisor, dizemos que a operação tem um resto. Esse resto é o número que sobra após a divisão.

Exemplo de divisão com resto:

$$23÷4=5\text{com resto}3$$

Aqui, 23 dividido por 4 dá um quociente de 5, mas sobram 3 unidades, ou seja, o resto é 3.

5. Divisão com Números Decimais

Caso o divisor não divida exatamente o dividendo, podemos continuar a divisão com números decimais, utilizando a casa decimal para obter uma resposta mais precisa.

Exemplo:

$$5÷2=2,5$$

Nesse caso, a divisão de 5 por 2 resulta em um número decimal, com 2,5 como quociente.

6. A Divisão e a Multiplicação Inversa

A divisão é, na verdade, a operação inversa da multiplicação. Isso significa que, se você tem uma multiplicação, pode encontrar a divisão que corresponde a essa operação. Por exemplo:

• Se 2 × 3 = 6, então 6 ÷ 3 = 2.
• Se 7 × 4 = 28, então 28 ÷ 4 = 7.

Isso nos permite resolver problemas de divisão de forma mais eficiente, especialmente ao trabalhar com frações e decimais.

7. Divisão de Frações

A divisão de frações é uma operação importante, onde, para dividir uma fração por outra, basta multiplicar a primeira fração pelo inverso da segunda. O inverso de uma fração é obtido trocando o numerador pelo denominador.

Exemplo:

23÷45=23×54=1012=56\frac{2}{3} ÷ \frac{4}{5} = \frac{2}{3} × \frac{5}{4} = \frac{10}{12} = \frac{5}{6}32​÷54​=32​×45​=1210​=65​

Conclusão:

A divisão é uma operação matemática essencial que nos permite distribuir uma quantidade em partes iguais. Além de ser a operação inversa da multiplicação, a divisão nos ajuda a entender melhor as relações entre os números. Ela pode ser exata ou deixar um resto, e é a base para trabalhar com números fracionários e decimais. Compreender os elementos da divisão e suas regras é fundamental para a solução de diversos problemas matemáticos.